
AC Waveform and AC Circuit Theory
Related Terms
The Period, (T) is the length of time in seconds that the waveform takes to repeat itself from start to finish. This can also be called the Periodic Time of the waveform for sine waves, or the Pulse Width for square waves.
The Frequency, (ƒ) is the number of times the waveform repeats itself within a one second time period. Frequency is the reciprocal of the time period, ( ƒ = 1/T ) with the unit of frequency being the Hertz, (Hz).
The Amplitude (A) is the magnitude or intensity of the signal waveform measured in volts or amps.
In our tutorial about Waveforms ,we looked at different types of waveforms and said that “Waveforms are basically a visual representation of the variation of a voltage or current plotted to a base of time”. Generally, for AC waveforms this horizontal base line represents a zero condition of either voltage or current. Any part of an AC type waveform which lies above the horizontal zero axis represents a voltage or current flowing in one direction.
Likewise, any part of the waveform which lies below the horizontal zero axis represents a voltage or current flowing in the opposite direction to the first. Generally for sinusoidal AC waveforms the shape of the waveform above the zero axis is the same as the shape below it. However, for most non-power AC signals including audio waveforms this is not always the case.
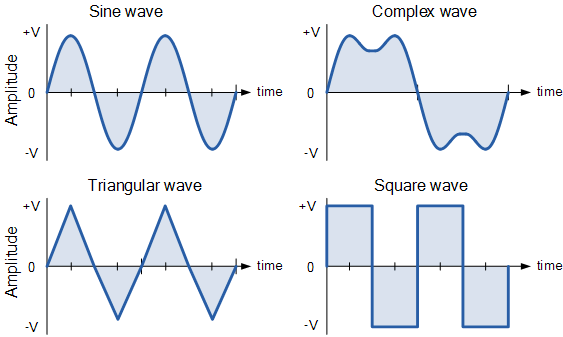
The most common periodic signal waveforms that are used in Electrical and Electronic Engineering are the Sinusoidal Waveforms. However, an alternating AC waveform may not always take the shape of a smooth shape based around the trigonometric sine or cosine function. AC waveforms can also take the shape of either Complex Waves, Square Waves or Triangular Waves and these are shown below.
Amplitude of an AC Waveform
As well as knowing either the periodic time or the frequency of the alternating quantity, another important parameter of the AC waveform is Amplitude, better known as its Maximum or Peak value represented by the terms, Vmax for voltage or Imax for current.
The peak value is the greatest value of either voltage or current that the waveform reaches during each half cycle measured from the zero baseline. Unlike a DC voltage or current which has a steady state that can be measured or calculated using Ohm’s Law, an alternating quantity is constantly changing its value over time.
For pure sinusoidal waveforms this peak value will always be the same for both half cycles ( +Vm = -Vm ) but for non-sinusoidal or complex waveforms the maximum peak value can be very different for each half cycle. Sometimes, alternating waveforms are given a peak-to-peak, Vp-p value and this is simply the distance or the sum in voltage between the maximum peak value, +Vmax and the minimum peak value, -Vmax during one complete cycle.